Power approximations for overall average effects in meta-analysis of dependent effect sizes
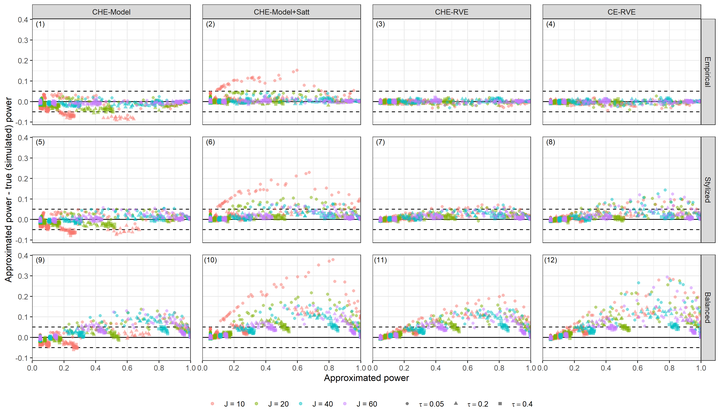Power difference between approximated and true (simulated) power versus approximated power for the C(H)E working models, across different methods of sampling study characteristics.
Abstract
Meta-analytic models for dependent effect sizes have grown increasingly sophisticated over the last few decades, which has created challenges for a priori power calculations. We introduce power approximations for tests of average effect sizes based upon several common approaches for handling dependent effect sizes. In a Monte Carlo simulation, we show that the new power formulas can accurately approximate the true power of meta-analytic models for dependent effect sizes. Lastly, we investigate the Type I error rate and power for several common models, finding that tests using robust variance estimation provide better Type I error calibration than tests with model-based variance estimation. We consider implications for practice with respect to selecting a working model and an inferential approach.