James E. Pustejovsky

I am a statistician and associate professor in the School of Education at the University of Wisconsin-Madison, where I teach in the Educational Psychology Department and the graduate program in Quantitative Methods. My research involves developing statistical methods for problems in education, psychology, and other areas of social science research, with a focus on methods related to research synthesis and meta-analysis.

Interests

  • Meta-analysis
  • Causal inference
  • Robust statistical methods
  • Education statistics
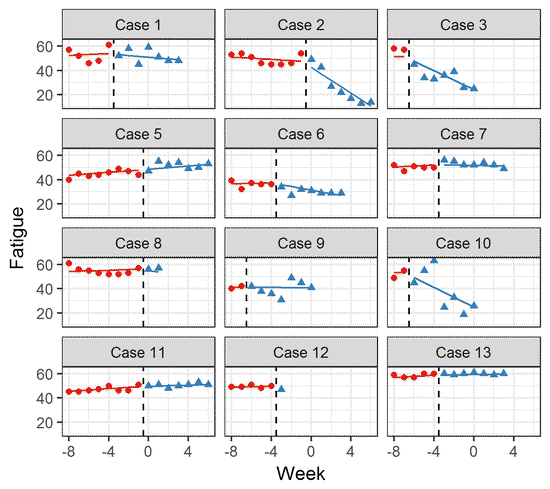
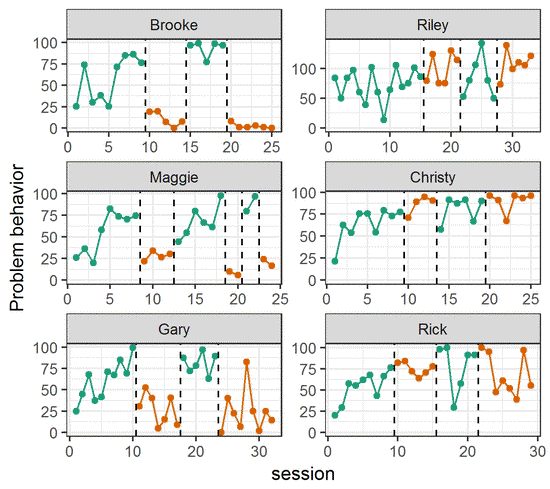
  • Single case experimental designs

Education

  • PhD in Statistics, 2013

    Northwestern University

  • BA in Economics, 2003

    Boston College

Recent Posts

2022-11-07

Corrigendum to Pustejovsky and Tipton (2018), redux

\[ \def\Pr{{\text{Pr}}} \def\E{{\text{E}}} \def\Var{{\text{Var}}} \def\Cov{{\text{Cov}}} \def\bm{\mathbf} \def\bs{\boldsymbol} \] In my 2018 paper with Beth Tipton, published in the Journal of Business and Economic Statistics, we considered how to do cluster-robust variance estimation in fixed effects models estimated by weighted (or unweighted) least squares.

2022-09-28

Corrigendum to Pustejovsky and Tipton (2018)

\[ \def\Pr{{\text{Pr}}} \def\E{{\text{E}}} \def\Var{{\text{Var}}} \def\Cov{{\text{Cov}}} \def\bm{\mathbf} \def\bs{\boldsymbol} \] In my 2018 paper with Beth Tipton, published in the Journal of Business and Economic Statistics, we considered how to do cluster-robust variance estimation in fixed effects models estimated by weighted (or unweighted) least squares.

2021-11-28

Variance component estimates in meta-analysis with mis-specified sampling correlation

\[ \def\Pr{{\text{Pr}}} \def\E{{\text{E}}} \def\Var{{\text{Var}}} \def\Cov{{\text{Cov}}} \] In a recent paper with Beth Tipton, we proposed new working models for meta-analyses involving dependent effect sizes. The central idea of our approach is to use a working model that captures the main features of the effect size data, such as by allowing for both between- and within-study heterogeneity in the true effect sizes (rather than only between-study heterogeneity).

2021-11-02

Implications of mean-variance relationships for standardized mean differences

I spend more time than I probably should discussing meta-analysis problems on the R-SIG-meta-analysis listserv. The questions that folks pose there are often quite interesting—especially when they’re motivated by issues that they’re wrestling with while trying to complete meta-analysis projects in their diverse fields.

2021-10-20

Inverting partitioned matrices

There’s lots of linear algebra out there that’s quite useful for statistics, but that I never learned in school or never had cause to study in depth. In the same spirit as my previous post on the Woodbury identity, I thought I would share my notes on another helpful bit of math about matrices.

See all posts

Working papers

Between-case standardized mean differences: Flexible methods for single-case designs

Single-case designs (SCDs) are a class of research methods for evaluating the effects of academic and behavioral interventions in educational and clinical settings. Although visual analysis is …
Preprint Code Supplementary materials

Comparison of competing approaches to analyzing cross-classified data: Random effects models, ordinary least squares, or fixed effects with cluster robust standard errors

Cross-classified random effects modeling (CCREM) is a common approach for analyzing cross-classified data in education. However, when the focus of a study is on the regression coefficients at level …
Preprint Supplementary materials

High replicability of newly-discovered social-behavioral findings is achievable.

Failures to replicate evidence of new discoveries have forced scientists to ask whether this unreliability is due to suboptimal implementation of optimal methods or whether presumptively optimal …
Preprint Supplementary materials

Recent Publications

Power approximations for overall average effects in meta-analysis of dependent effect sizes

Meta-analytic models for dependent effect sizes have grown increasingly sophisticated over the last few decades, which has created challenges for a priori power calculations. We introduce power …
Preprint Code Journal Supplementary materials R package

Investigating narrative performance in children with developmental language disorder: A systematic review and meta-analysis

Purpose: Speech-language pathologists (SLPs) typically examine narrative performance when completing a comprehensive language assessment. However, there is significant variability in the methodologies …
Preprint Code Dataset Journal Supplementary materials

Multi-level meta-analysis of single-case experimental designs using robust variance estimation

Single-case experimental designs (SCEDs) are used to study the effects of interventions on the behavior of individual cases, by making comparisons between repeated measurements of an outcome under …
Preprint Code Journal Supplementary materials

Augmentative and Alternative Communication intervention targets for school-aged participants with ASD and ID: A single-case systematic review and meta-analysis

Objective: This meta-analysis reviews the literature on communication modes, communicative functions, and types of augmentative and alternative communication (AAC) interventions for school-age …
Preprint Code Dataset Journal

Considering instructional contexts in AAC interventions for people with ASD and/or IDD experiencing complex communication needs: A single-case design meta-analysis

For children with autism or intellectual and developmental disabilities who also have complex communication needs, communication is a necessary skill set to increase independence and quality of life. …
Preprint Code Dataset Journal
See all publications

Recent Presentations

A matter of emphasis: Comparison of working models for meta-analysis of dependent effect sizes

2022-07-20 2:50 PM Society for Research Synthesis Methodology annual meeting Portland, OR (and online)
Slides

The state of single case synthesis: Premises, tools, and possibilities

2022-05-19 1:00 PM Spencer Single Case Conference Vanderbilt University, Nashville, TN
Slides

Selective reporting in meta-analysis of dependent effect size estimates

Publication bias and other forms of selective outcome reporting are important threats to the validity of findings from research syntheses—even undermining their special status for informing evidence-based practice and policy guidance.
2022-02-08 6:00 PM Stanford Quantitative Sciences Unit Research Methods Seminar online
Slides

Easy, cluster-robust standard errors with the clubSandwich package

Cluster-robust variance estimation methods (also known as sandwich estimators, linearization estimators, or simply “clustered” standard errors) are a standard inferential tool in many …
2022-02-03 10:00 AM Oslo R User Group Meetup online
Slides Video

Four things every quantitative social scientist should know about meta-analysis

Meta-analysis is a set of statistical tools for synthesizing results across multiple sources of evidence. Meta-analyses of intervention research are often taken as a gold standard for informing …
2021-09-27 10:00 AM Educational Psychology PIE Colloquium Educational Sciences 259
Slides
See all talks

Software

POMADE

Power for Meta-Analysis of Dependent Effects

lmeInfo

Information Matrices for ‘lmeStruct’ and ‘glsStruct’ Objects

simhelpers

Helper package to assist in running simulation studies

ARPobservation

Simulate systematic direct observation data

clubSandwich

Cluster-robust variance estimation

scdhlm

Between-case SMD for single-case designs

SingleCaseES

Single-case design effect size calculator

wildmeta

Cluster-wild bootstrap for meta-regression

Students

Current Advisees

Avatar

Man Chen

Graduate student

Avatar

Young Ri Lee

Graduate student

Avatar

Paulina Grekov

Graduate student

Alumni

Avatar

Megha Joshi

Quantitative Researcher

Avatar

Christopher Runyon

Measurement Scientist

Mascot

Avatar

Whatev's Donkey

Lab mascot

Teaching

At UW Madison

At UT Austin

Contact

Topics

AERA alternating renewal process Augmentative and alternative communication behavioral observation bootstrap cancer causal inference correlation delta method dependent effect sizes design-comparable SMD developmental language disorder distribution theory econometrics effect size evaluation experimental design fixed effects generalized linear model heterogeneity hierarchical models hypothesis testing instrumental variables inter-rater reliability matrix algebra meaning and purpose mental health meta-analysis meta-regression missing data multivariate narrative assessment nlme non-linear model non-overlap measures panel data physical health positive affect power pre-registration programming psycho-social intervention publication bias question-order random effects regression discontinuity religion/spirituality replication response ratio response-guided design robust variance estimation Rstats sandwiches self-efficacy simulation single-case design small-sample social health social networks standardized mean difference Stata systematic review TACC Transition to College Mathematics transportation weighting