Evaluating meta-analytic methods to detect selective reporting in the presence of dependent effect sizes
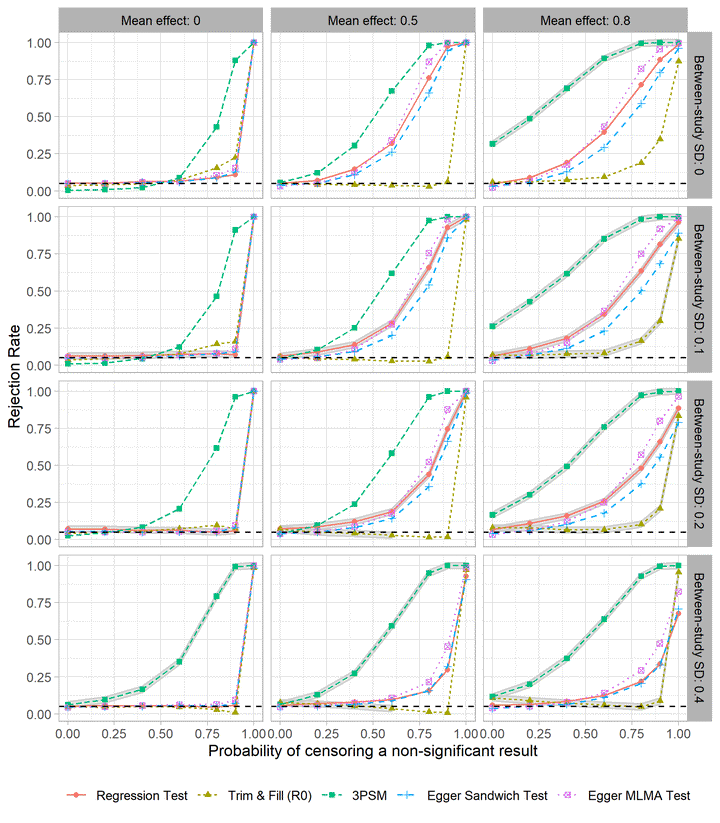 Power of tests for selective reporting when dependent effects are aggregated or handled using Robust Variance Estimation (RVE) or Multi-Level Meta-Analysis (MLMA), for samples of $k = 80$ studies and between study correlation of $\rho = 0.4$. Gray bands indicate tests with excess Type-I error.
Power of tests for selective reporting when dependent effects are aggregated or handled using Robust Variance Estimation (RVE) or Multi-Level Meta-Analysis (MLMA), for samples of $k = 80$ studies and between study correlation of $\rho = 0.4$. Gray bands indicate tests with excess Type-I error.
Abstract
Meta-analysis is a set of statistical tools used to synthesize results from multiple studies evaluating a common research question. Two methodological challenges when conducting meta-analysis include selective reporting and correlated dependent effect sizes. Selective reporting is often a result of selective publication practices based on the statistical significance of study findings, which threatens the validity of meta-analytic results. One of the main sources of dependent effect sizes is the inclusion of multiple outcome measures from a primary study. This violates conventional, univariate meta-analytic techniques. Meta-analysts lack validated methods to detect the presence of selective reporting while incorporating methods to handle dependent effect sizes. This study evaluates currently available univariate selective reporting methods, when ignoring dependence, selecting one effect size per study, or aggregating dependent correlated effect sizes. This study also proposes and examines an Egger’s Regression variant incorporated with Robust Variance Estimation (RVE) to handle within-study dependence. A Monte Carlo simulation study assess the performance of the methods for Type I error rates in the absence of selective reporting, and power to detect selective reporting when introduced. Ignoring dependence inflates Type I error rates for all univariate detection methods. Type I error rates are maintained with regression tests when dependent effect sizes are sampled, aggregated or modeled using RVE. However, all selective reporting methods evaluated in this study have little to no power to detect selection bias, except under strong selection censoring.